크래프톤 정글 6기 TIL - Day 15 | DP, 그리디, LCS
by 브이담곰
Dynamic Programming(DP)
동적 프로그래밍
정의 : 여러개의 하위 문제를 먼저 푼 후 그 결과를 쌓아올려 주어진 문제를 해결하는 알고리즘.
ex) 피보나치 수열
1️⃣ 재귀로 풀 때
💡 재귀로 푼 다면 메모리 사용이 많이 커지고 같은 값을 중복으로 구하는 연산이 포함되어 있을 수 있어서 비효율적이다.
def fibo(n):
if n <= 1:
return 1
return fibo(n-1) + fibo(n-2)2️⃣ DP를 사용했을 때
-1- Top Down 방식( Memorization) : 재귀
재귀를 사용하지만 배열에 값을 저장해두기때문에 한번 구한 값은 다시 구하지 않아도 된다.
def fibo(n, memo):
if n <= 1:
return 1
if memo not in n:
memo[n] = fibo(n-1) + fibo(n-2)
return memo[n]
-2- Bottom Up 방식: for문
O(1) 의 시간복잡도로 최종 값을 구할 수 있다.
def fibo(N):
if n < 2:
return 1
fibo = [0]*N
fibo[0] = 1
fibo[1] = 1
for n in range(2, N):
fibo[n]= fibo[n-1]+fibo[n-2]
return fibo[n]
이 처럼 작은 문제들을 푼 결과들을 이용해 큰 문제를 푸는 것이 동적 프로그래밍이다.
DP를 푸는 과정
1. 테이블 정의하기
2. 점화식 찾기
3. 초기값 정하기
#1463 1로 만들기

1. 테이블 정의하기
D[ i ] = i를 1로 만들기 위해 필요한 연산 횟수 최솟값
2. 점화식 찾기
D[12] = ?
(1) D[12] = D[4] + 1
(2) D[12] = D[6] + 1
(3) D[12] = D[11] + 1
→ D[12] = min(D[4]+1, D[6] + 1, D[11] + 1)
3. 초기값 정하기
D[1] = 0 #1이므로 아무것도 안해도 된다!
Greedy Algorithm
그리디 알고리즘
1. Greedy Choice Property
각 단계에서 '최선의 선택'을 했을 때 전체 문제에 대한 최적해를 구할 수 있는 경우를 말함.
2. Optimal Substructure
전체 문제의 최적해가 '부분 문제의 최적해로 구성' 될 수 있는 경우를 말함. → 전체 문제를 작은 부분 문제로 나누어 각각의 문제에서 최적해를 구한 후 이를 조합하여 전체 문제의 최적해를 구하는 것을 의미
LCS(Longest Common Subsequence)
최장 공통 부분 수열
최장 공통 문자열

두 문자열의 문자를 하나씩 비교한다.


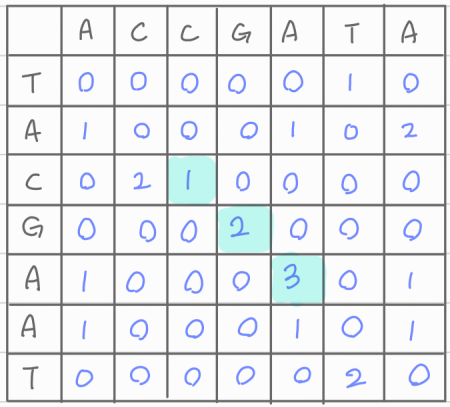
최장 공통 시퀸스

문자열과 비슷하게 아래와 같은 조건식을 세울 수 있다.



최장 공통 시퀸스 찾기

1. LCS 배열 가장 마지막 값을 시작으로 둔다
2. LCS[i-1][j], LCS[i][j-1] 중 현재값과 같은 값 찾기
2-1. 같은 값이 있다면 해당 배열로 이동한다.
2-2. 다른 값이라면 result에 해당 문자를 넣고, LCS[i-1][j-1]로 이동
3. 2번을 반복하다 0이 되면 종료한다.
위의 과정을 통해 아래의 배열을 얻을 수 있고, 이를 reverse하면 답을 얻을 수 있다!!!

9251.LCS
https://www.acmicpc.net/problem/9251
import sys
input = sys.stdin.readline
# 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제.
A = list(input().rstrip())
B = list(input().rstrip())
LCS = [[0 for _ in range(len(A) + 1)] for _ in range((len(B) + 1))]
for i in range(1, len(B) + 1):
for j in range(1, len(A) + 1):
if A[j - 1] == B[i - 1]: # 만약 같을 경우는 +1 해준다 허허 인덱스 행렬이 넘 헷갈리네ㅠㅜ실수가 한두번이아니네 넘 슬프다ㅜ
# A[i-1] == B[j-1] 이렇게 해서 매치가 안됐음 ㅠㅜ
LCS[i][j] = LCS[i - 1][j - 1] + 1
else:
LCS[i][j] = max(LCS[i][j - 1], LCS[i - 1][j])
# for L in LCS:
# print(L)
print(LCS[len(B)][len(A)])'KRAFTON JUNGLE > JUNGLE TIL' 카테고리의 다른 글
| 크래프톤 정글 6기 TIL - Day 17 | 포인터(pointer), & 연산자와 * 연산자 (0) | 2024.07.26 |
|---|---|
| 크래프톤 정글 6기 TIL - Day 16 | Knapsack Problem (0) | 2024.07.20 |
| 크래프톤 정글 6기 TIL - Day 14 | 다익스트라, 플로이드 와샬 (3) | 2024.07.16 |
| 크래프톤 정글 6기 TIL - Day 13| 최소 신장 트리, 유니온 알고리즘 (0) | 2024.07.14 |
| 크래프톤 정글 6기 TIL - Day 12| 위상 정렬 (0) | 2024.07.12 |
블로그의 정보
농담곰담곰이의곰담농
브이담곰