크래프톤 정글 6기 TIL - Day 14 | 다익스트라, 플로이드 와샬

오늘은 치밥을 먹엇다.

 

---

다익스트라

다익스트라 알고리즘: 하나의 시작점으로부터 다른 모든 정점까지의 최단거리를 구하는 알고리즘

* 음수인 가중치를 가진 간선이 있다면 사용할 수 없다.

 

구현

1. 자기 자신과의 거리는 0이므로 ① 번 인덱스의 값은 0으로 둔다.

2. ①번 정점에서는 ②, ③ ,④ 번 정점으로만 갈 수 있는데, 최단거리 테이블에 3,2,5를 일단 써놓는다. (확정은 아님!)

최단 거리 테이블을 d라고 했을 때, d[2]~d[6] 까지 최솟값을 찾아서 최단거리를 확정한다.

 

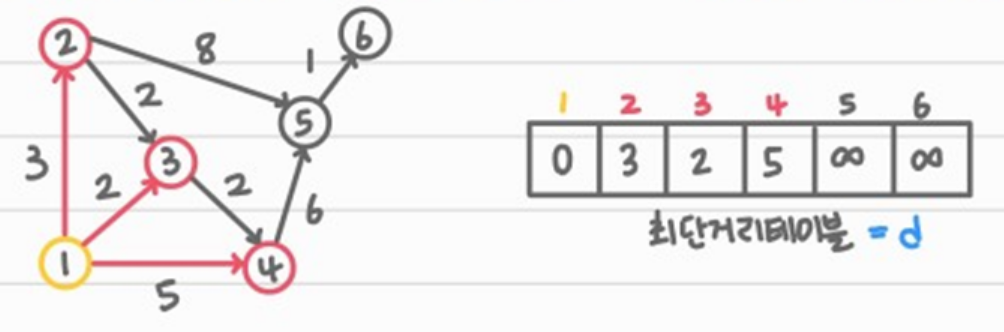
3. ③ 번 정점의 거리를 확정한 후 , 최단거리 테이블을 갱신한다.

① 번 정점에서의 간선은 이미 확인 했기 때문에 ③ 번 정점에서 뻗어나가는 간선만 본다.①②③

 

4. 가장 가까운 정점을 찾기 위해 d[2],d[4],~d[6] 확인.

 

5. 확정된 ④에서의 간선은 ⑤까지의 간선 1개이고 기존 11보다 d[4]+6이 더 작기때문에 갱신한다.

 

6. ⑥ 정점까지의 거리는 11로 바로 확정가능하다.

 

시간복잡도는 O(ElogE) 

 

플로이드 마샬

플로이드 알고리즘: 모든 정점 쌍 사이의 최단거리를 구하는 알고리즘

인접되어 있는 정점의 간선의 가중치를 테이블에 입력한다.

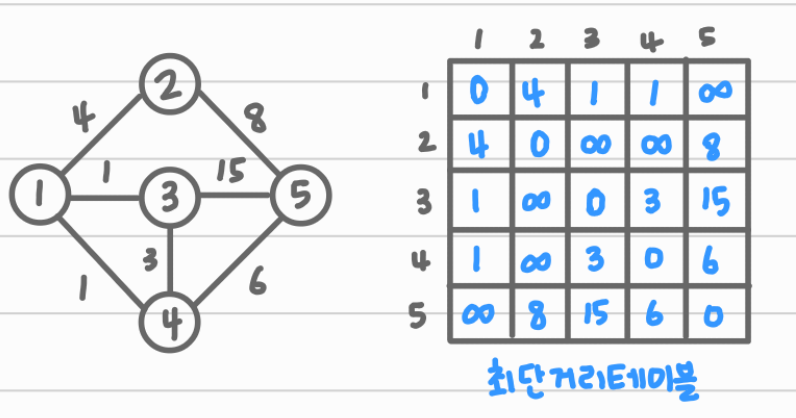
S에서 T로 갈 때 1번 정점을 거쳐가는 최단거리? D[S][1] + D[1][T]

D[S][T] > D[S][1] + D[1][T] 일 경우에만 테이블을 갱신한다.

D[S][T] >  D[S][2] + D[1][2]일 경우에만 갱신

 

현재 테이블에 적힌 값은 중간에 다른 정점을 거치지 않았거나 1,2번 정점을 거쳐서 갈 때의 최단거리이다.

 

위의 과정을 1~V까지 반복하면 된다.

 

시간 복잡도는 O(n^3)이다.

 

경로 복원 방법

위 처럼 최단거리테이블을 이용해 최단 거리를 구할 수 있다. 하지만 어떤 경로로 최단거리가 되는지는 알 수 없다.

경로 복원 방법을 통해 어떤 순서로 정점을 거쳐야 최단 거리로 목적지까지 이동할 수 있는지 계산한다.

nxt테이블은 a에서 b까지 최단거리로 가려면 a에서 어느 정점으로 가야하는지를 나타내는 테이블이다.

예를 들어,  'nxt[1][2] = 2' 는 1에서 2까지 최단거리로 가려면 가야하는 정점을 나타낸다.

인접 되어있는 정점들끼리는 서로가 최단거리 이기 때문에, 초기 nxt테이블에는 인접된 정점을 넣어주면된다.

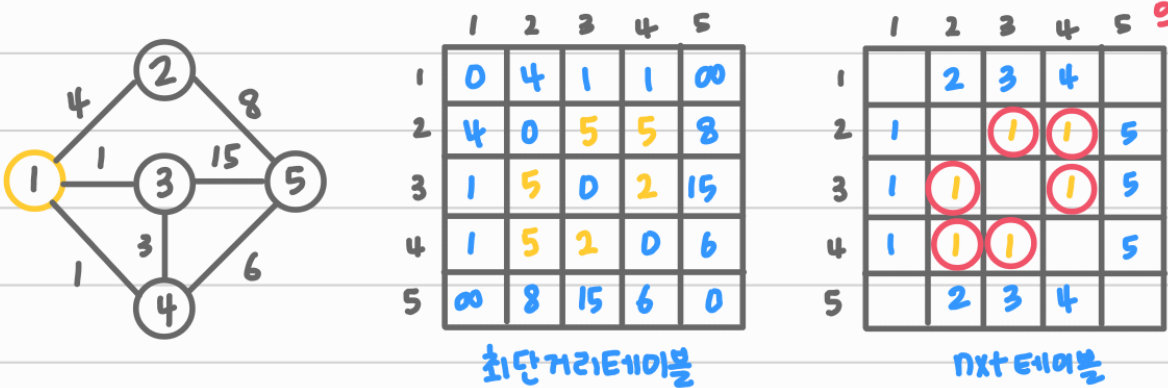
먼저, 최단거리 테이블에 D[S][T] > D[S][1] + D[1][T] 인 경로를 대체 해주고,

갱신된 좌표와 같이 nxt 테이블도 거치는 정점으로 갱신해준다.

D[2][3] > D[S][1] + D[1][T]  = INF > 5

D[2][4] > D[S][1] + D[1][T]  = INF > 5

D[3][2] > D[S][1] + D[1][T]  = INF > 5

D[3][4] > D[S][1] + D[1][T]  = INF > 2

D[4][2] > D[S][1] + D[1][T]  = INF > 5

D[4][3] > D[S][1] + D[1][T]  = INF > 2

그리고 갱신 된 좌표의 nxt테이블은 거쳐간 정점의 번호를 넣어준다.

D[S][T] > D[S][3] + D[3][T]  인 경로가 존재하지 않기 때문에 테이블에 변화 없다.

D[S][T] > D[S][4] + D[4][T]

D[S][T] > D[S][5] + D[5][T] 를 만족하는 경우가 없어 종료된다.

 

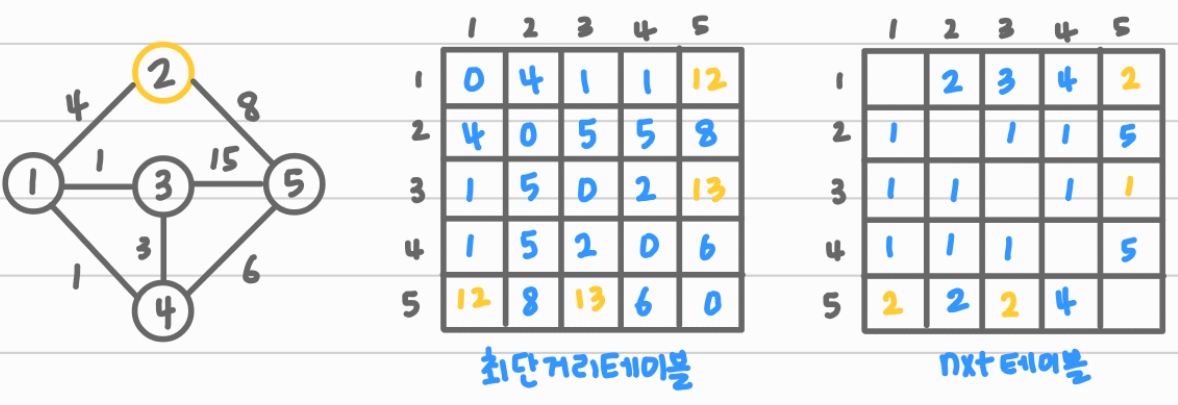
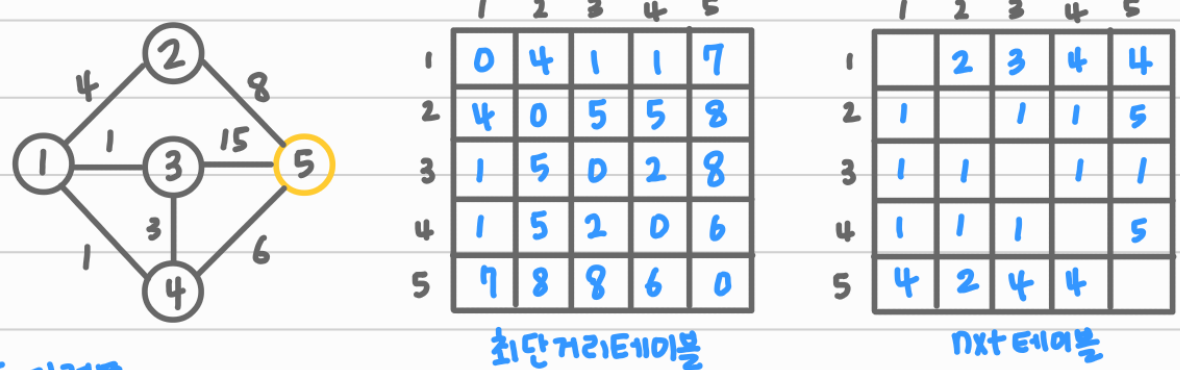
3 → 5로 가는 최단 경로를 구하려면 nxt 테이블로 추적가능하다.

1. nxt[3][5] = 1

2. nxt[1][5] = 4

3. nxt[4][5] = 5

1(D[3][1])+ 1(D[1][4]) + 6(D[4][5])